깎은 육팔면체
"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차
1. 개요
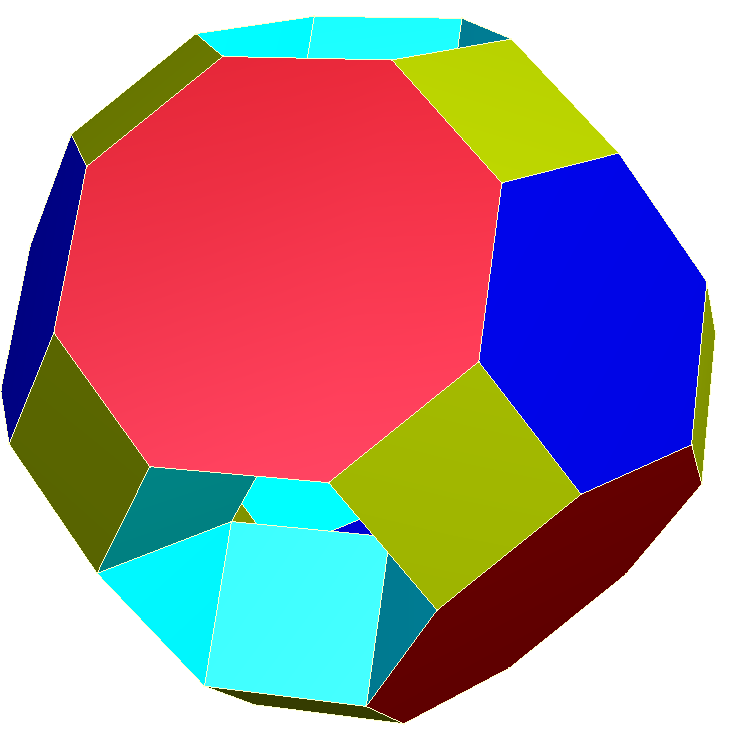
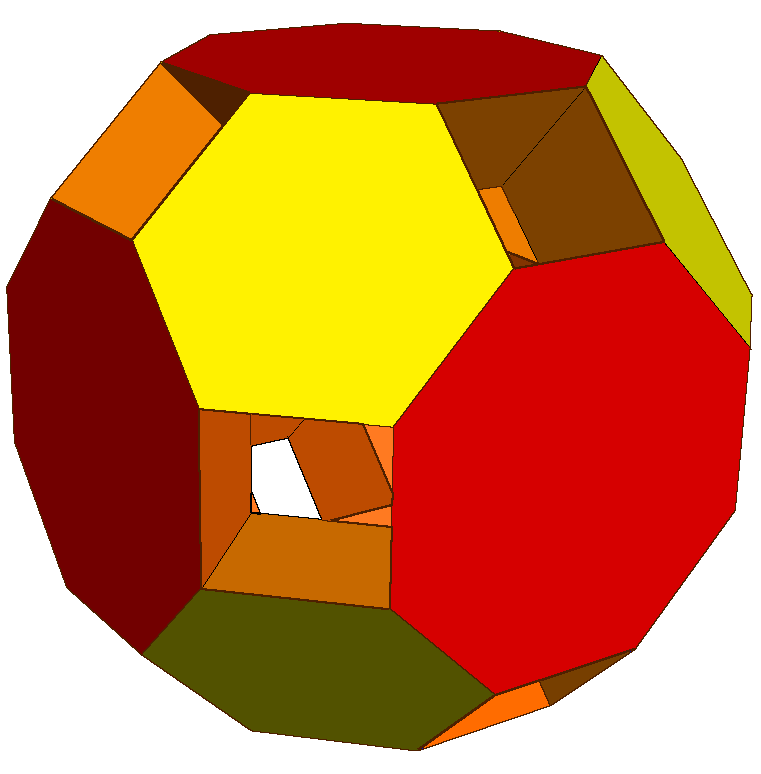
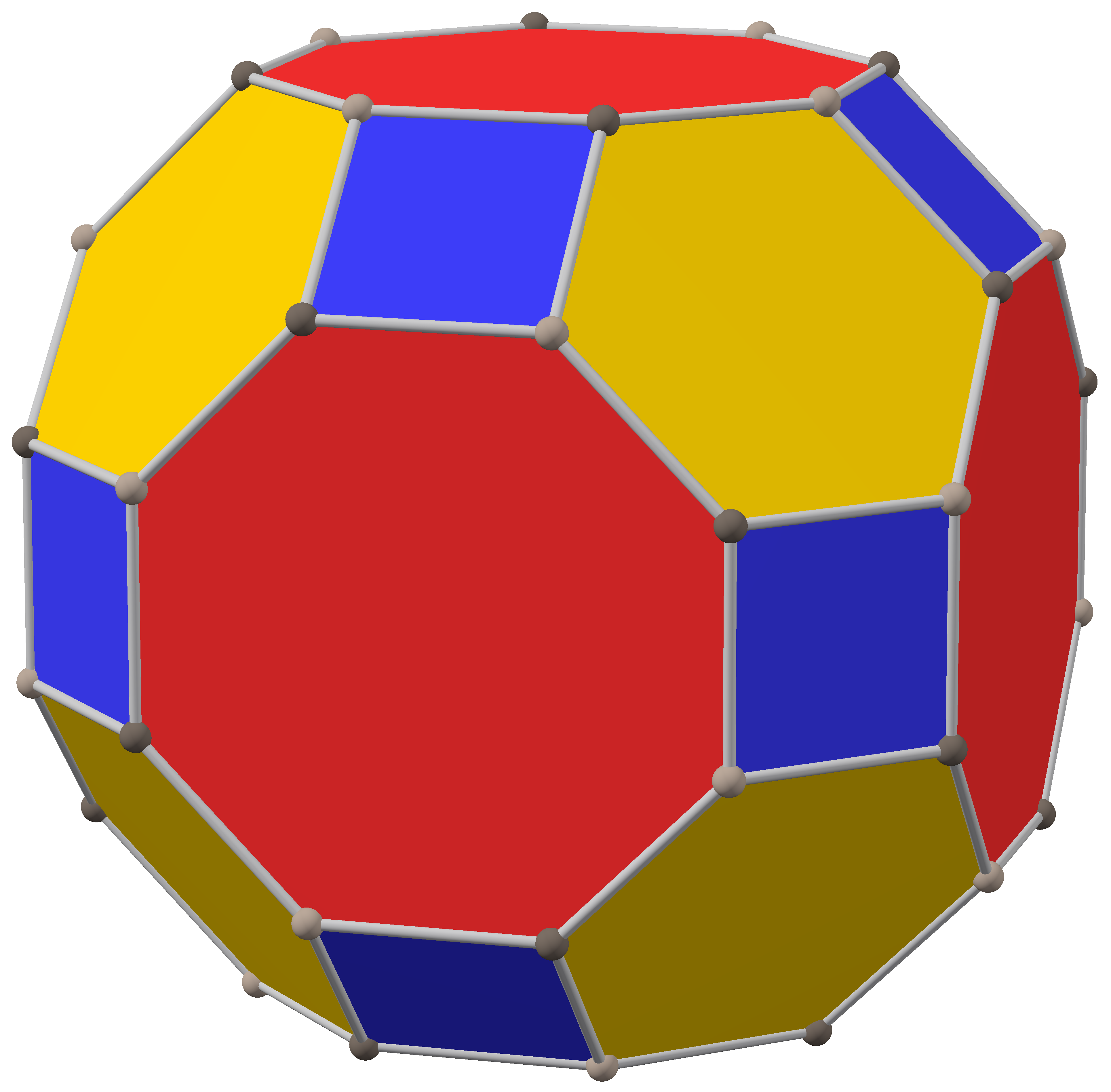
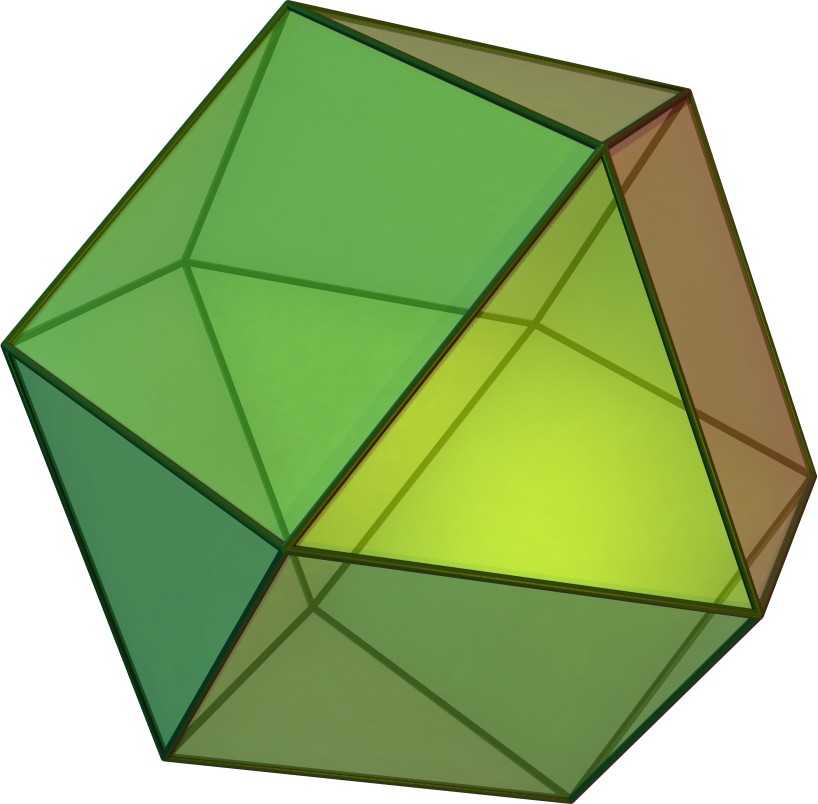
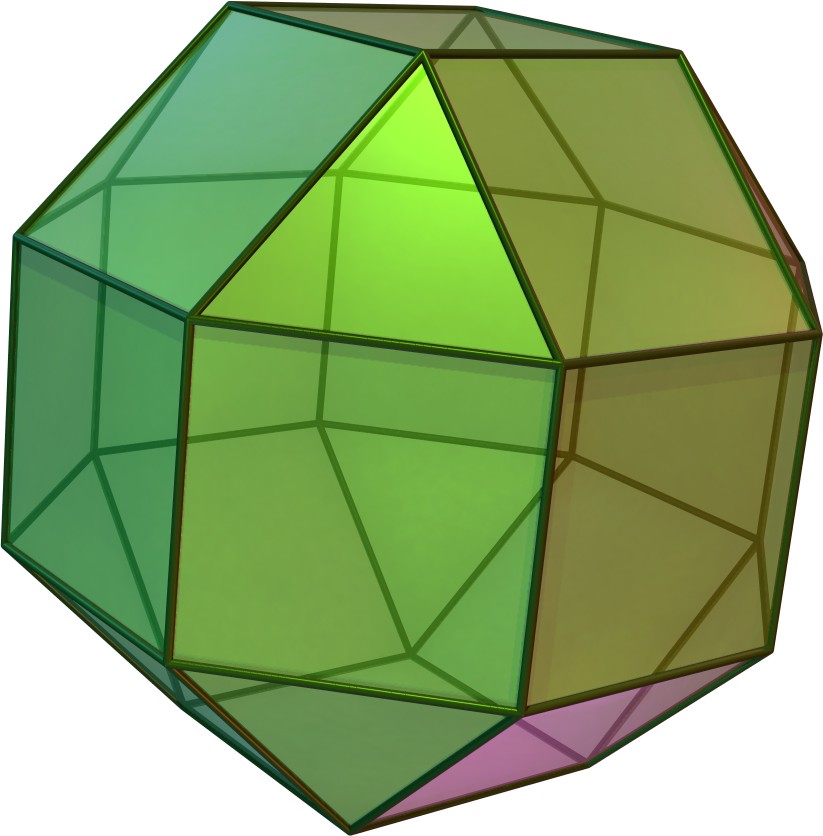
깎은 육팔면체는 깎은 육팔면체 그래프라고도 불리는 아르키메데스 깎은 다면체이다. 이 다면체는 48개의 꼭짓점과 72개의 모서리를 가지며, 겉넓이, 부피, 데카르트 좌표, 분할, 대칭성, 관련 다면체, 구면 타일링, 팔면체 대칭군, 그래프 이론과 같은 기하학적 성질을 갖는다.
더 읽어볼만한 페이지
| 깎은 육팔면체 | |
|---|---|
| 명칭 | |
| 영어 | 깎은 정육팔면체 (truncated cuboctahedron) |
| 다른 영어 명칭 | 마름모깎은 정육면체팔면체 (rhombitruncated cuboctahedron) 큰 마름모육팔면체 (great rhombicuboctahedron) |
| 기하학적 성질 | |
| 종류 | 반정다면체, 존 다면체 |
| 면의 수 | 26 |
| 면의 종류 | 정사각형: 12개, 정육각형: 8개, 정팔각형: 6개 |
| 변의 수 | 72 |
| 꼭짓점의 수 | 48 |
| 꼭짓점 배치 | 4, 6, 8 (정사각형 1개, 정육각형 1개, 정팔각형 1개) |
| 꼭짓점 도형 | Great rhombicuboctahedron vertfig.png |
| 슐레플리 기호 | tr{4, 3} |
| 위소프 기호 | |
| 대칭군 | Oh |
| 쌍대다면체 | 육방팔면체 |
| 성질 | 볼록 |
 | |
| |
| |
| |
2. 명칭
원래 요하네스 케플러가 명명한 ''깎은 육팔면체''라는 이름은 오해를 불러일으킬 수 있다. 실제 절단된 육팔면체는 정사각형 대신 직사각형 면을 가지기 때문이다. 그러나 이렇게 절단된 비균일 다면체는, 엄밀한 의미에서 깎은 육팔면체라고 불리는 아르키메데스의 다면체와 위상적으로 동일하다.
이 다면체를 부르는 다른 이름들은 다음과 같다.
- ''깎은 육팔면체'' (요하네스 케플러)
- ''마름모깎은 육팔면체'' (매그너스 웬닝거[1])
- ''큰 롬비큐보옥타헤드론'' (로버트 윌리엄스[2])
- ''큰 롬브큐보옥타헤드론'' (피터 크롬웰[3])
- ''옴니절단된 정육면체'' 또는 ''칸티절단된 정육면체'' (노먼 존슨)
- ''베벨 정육면체'' (콘웨이 다면체 표기법)
비슷한 이름을 가진 비볼록 균일 다면체로 비볼록 큰 롬비큐보옥타헤드론이 있다.
3. 기하학적 성질
깎은 육팔면체는 존 다면체의 일종이다.
3. 1. 데카르트 좌표
깎은 육팔면체의 모서리 길이가 2이고 원점에 중심을 둔 꼭짓점의 데카르트 좌표는 다음의 모든 순열이다.3. 2. 면적과 부피
변의 길이가 ''a''인 깎은 육팔면체의 면적 ''A''와 부피 ''V''는 다음과 같다.:
- 외접구 반지름: 한 변의 길이를 2라고 하면 이다.
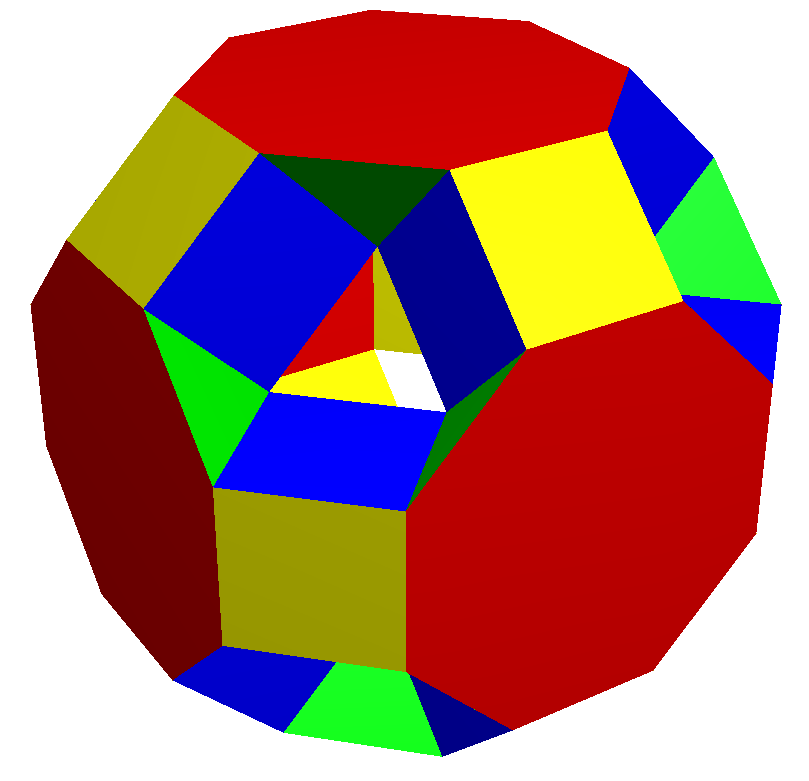
3. 3. 분할
깎은 육팔면체는 2겹 대칭축 위에 있는 12개의 정사각형 위에 육팔면체와 정육면체를 포함하는 볼록 껍질이다. 나머지 공간은 팔각형 아래에 6개의 정사각형 컵(square cupola)과 육각형 아래에 8개의 삼각 컵(triangular cupola)으로 나눌 수 있다.분해된 깎은 육팔면체는 중앙의 육팔면체와 6개의 정사각형 컵, 8개의 삼각 컵 또는 12개의 정육면체를 각각 제거하여 속 5, 7 또는 11의 스튜어트 토로이드를 만들 수 있다. 중앙 육팔면체와 다른 분해 구성 요소의 하위 집합을 제거하여 다른 많은 낮은 대칭 토로이드도 구성할 수 있다. 예를 들어, 삼각 컵 4개를 제거하면 속 3 토로이드가 생성된다. 이 컵을 적절하게 선택하면 이 토로이드는 사면체 대칭을 갖는다.[4][5]
| 스튜어트 토로이드 | |||
|---|---|---|---|
| 속 3 | 속 5 | 속 7 | 속 11 |
 |  |  |  |
4. 대칭성 및 관련 다면체
깎은 육팔면체는 아르키메데스의 다면체 중 하나로, 높은 수준의 대칭성을 지닌다. 이 다면체는 정육면체와 정팔면체의 대칭성을 공유하는 완전 팔면체 대칭(Oh)을 가지며, 이는 깎은 육팔면체의 구조와 특성을 이해하는 데 중요하다. 이러한 대칭성은 다면체의 균일 색칠, 직교 투영, 구면 타일링 표현 방식 등 다양한 기하학적 특징으로 나타난다. 또한, 깎은 육팔면체는 균일 다면체 및 존 다면체의 일원으로서 다른 여러 다면체 및 타일링과 밀접한 관계를 맺고 있다.
4. 1. 균일 색칠
이 다면체의 면에 대한 균일 색칠은 단 하나이며, 각 면 유형에 대해 하나의 색상이 사용된다.사면체 대칭을 갖는 2-균일 색칠은 육각형을 번갈아 가며 칠하는 방식으로 존재한다.
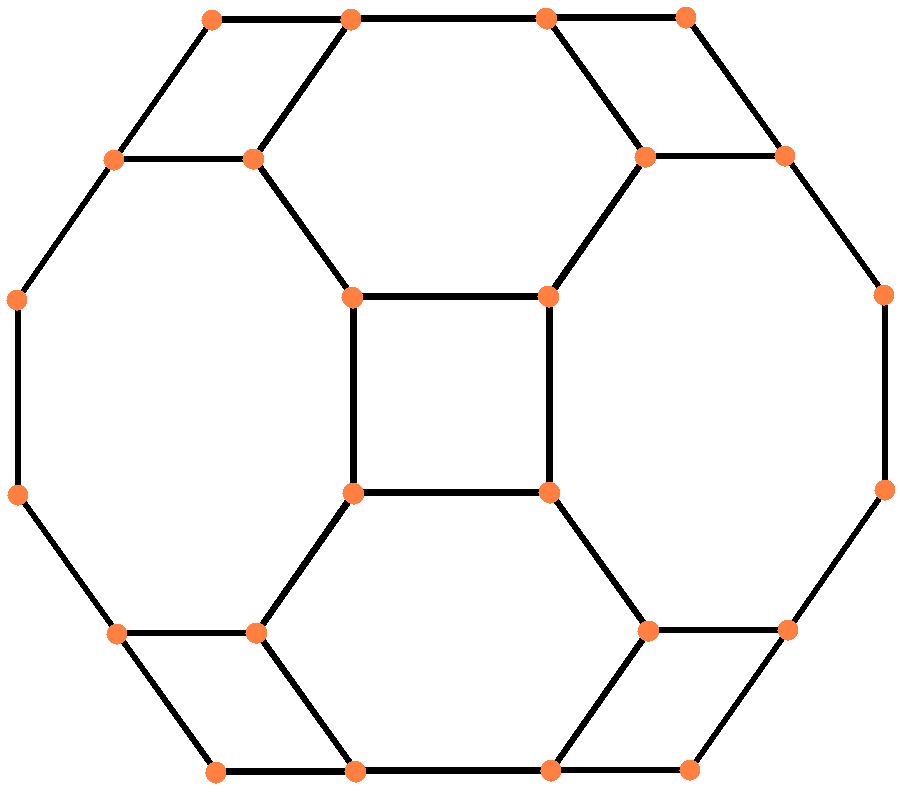
4. 2. 직교 투영
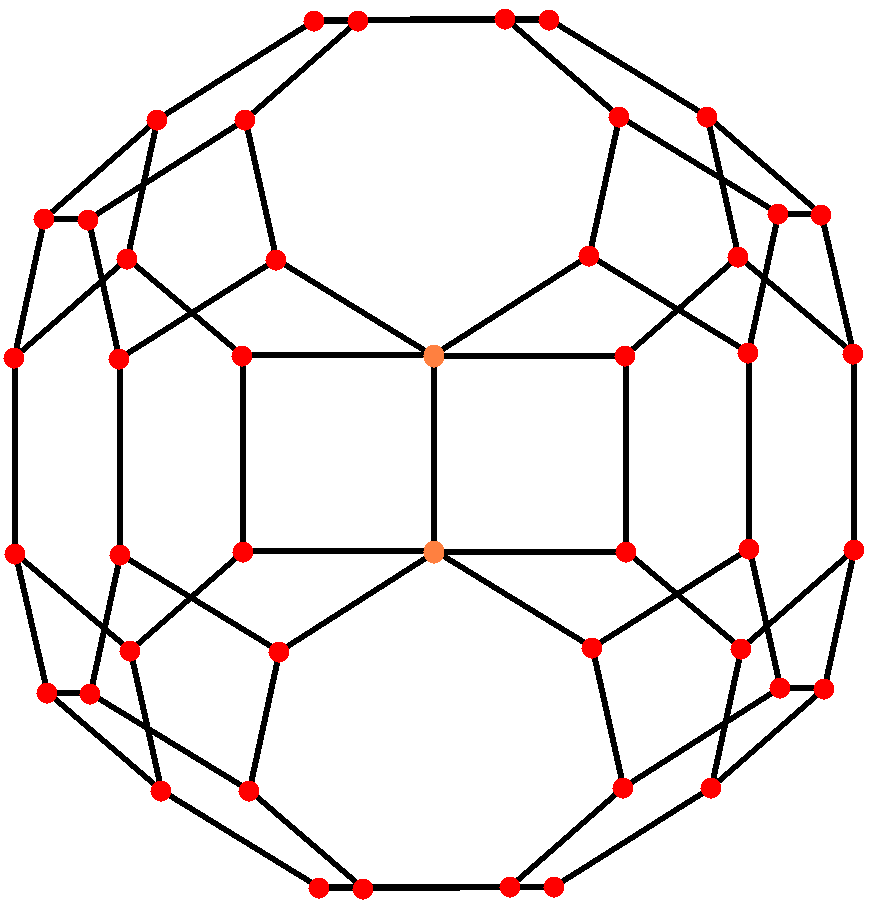
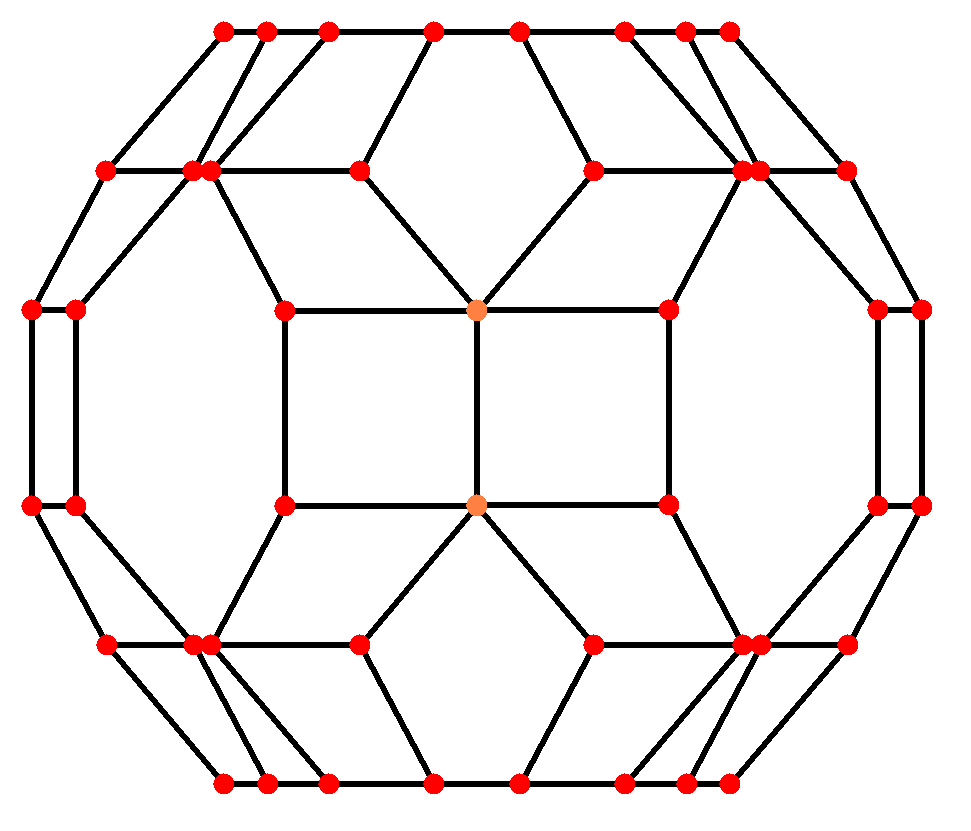
깎은 육팔면체는 A₂ 및 B₂ 코세터 평면에서 [6] 및 [8] 투영 대칭을 갖는 두 개의 특수한 직교 투영을 가지며, 다면체 요소와 관련된 다양한 투영 평면에서 수많은 [2] 대칭을 구성할 수 있다.| 중심 기준 | 꼭짓점 | 모서리 4-6 | 모서리 4-8 | 모서리 6-8 | 면 법선 4-6 |
|---|---|---|---|---|---|
| 이미지 |  |  |  |  |  |
| 투영 대칭 | [2]+ | [2] | [2] | [2] | [2] |
| 중심 기준 | 면 법선 정사각형 | 면 법선 팔각형 | 면 정사각형 | 면 육각형 | 면 팔각형 |
| 이미지 |  |  |  |  |  |
| 투영 대칭 | [2] | [2] | [2] | [6] | [4] |
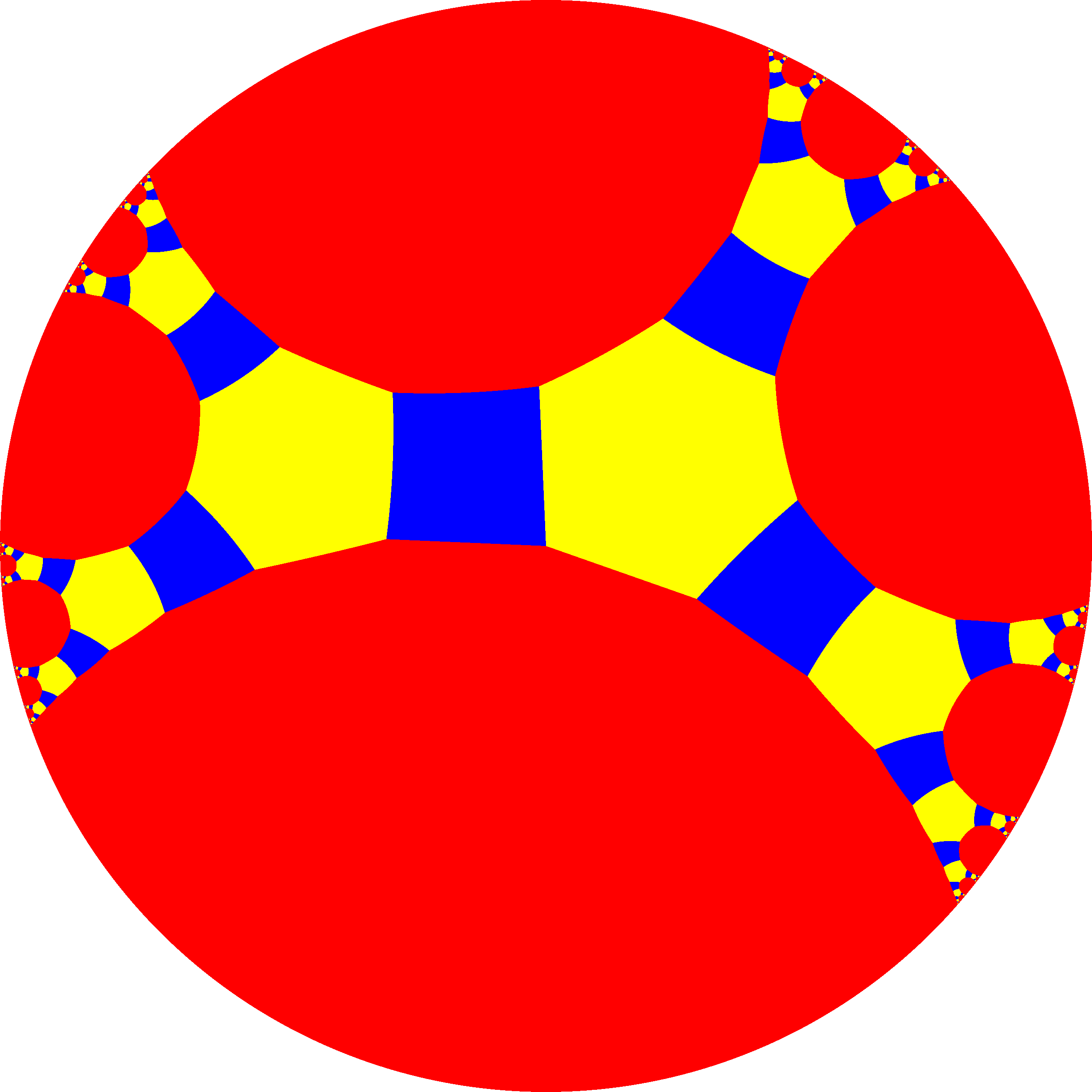
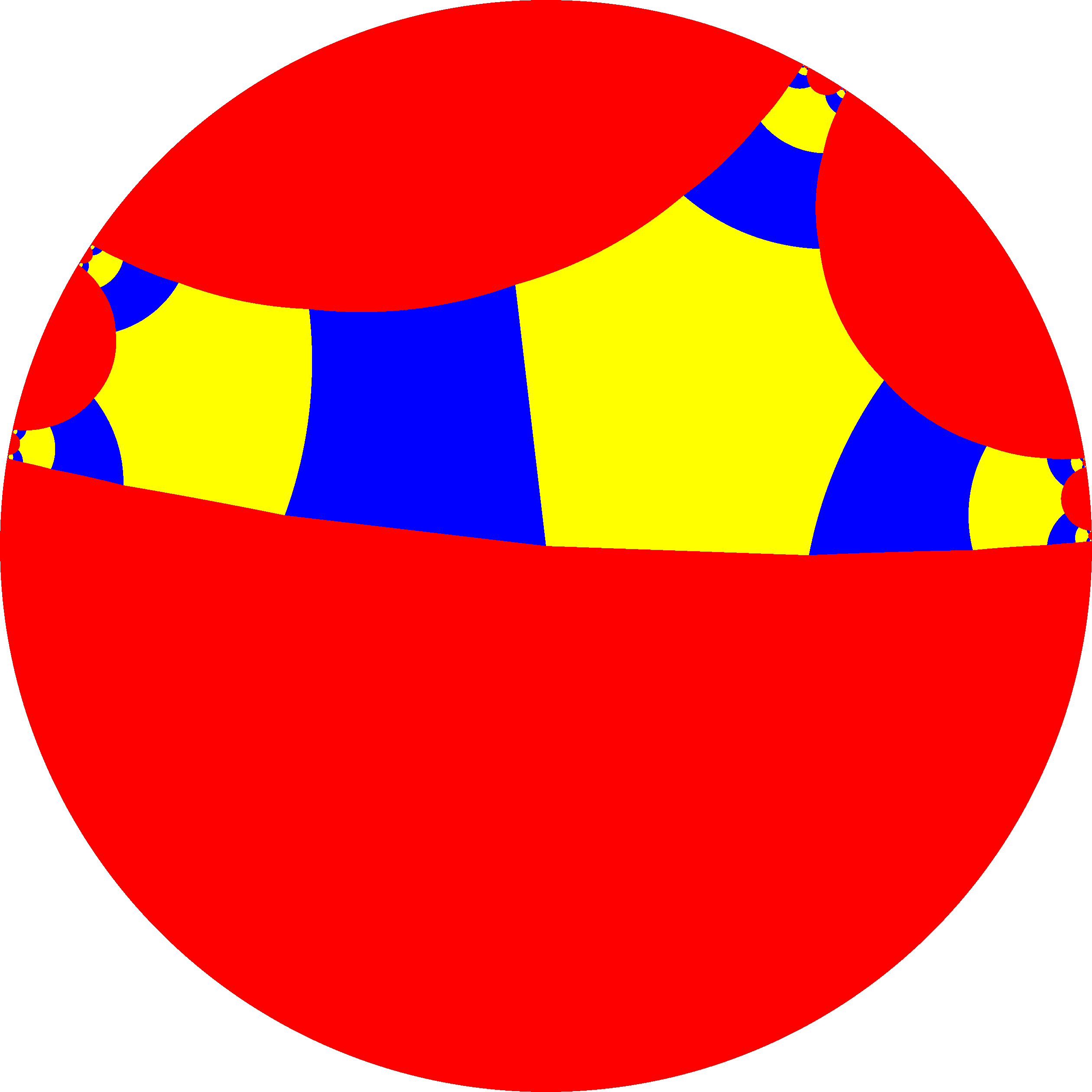
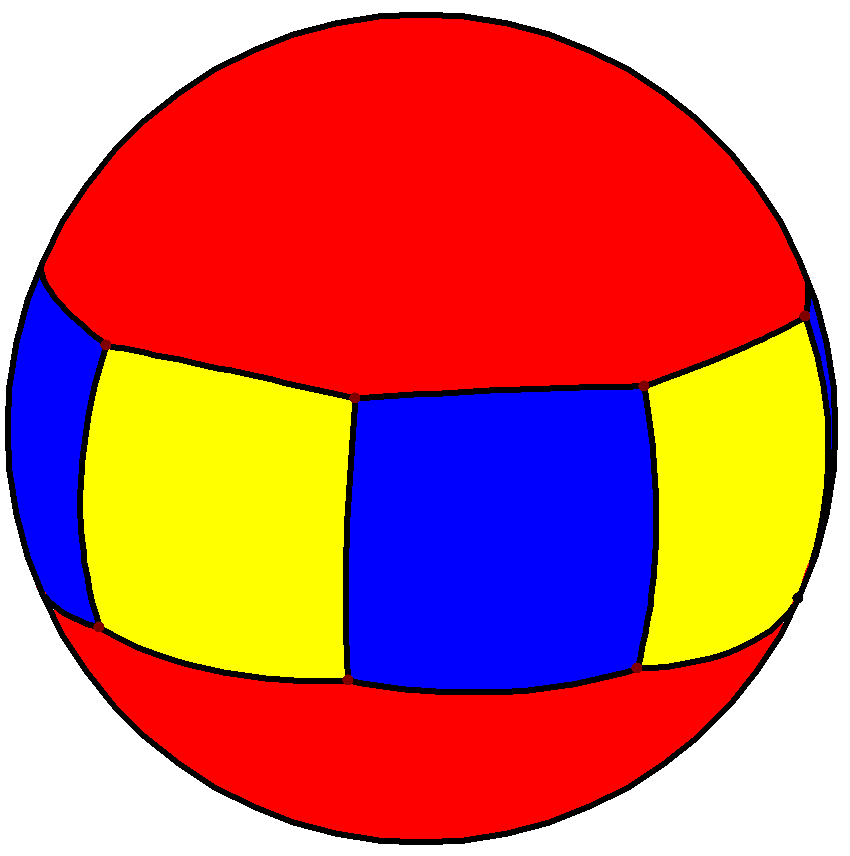
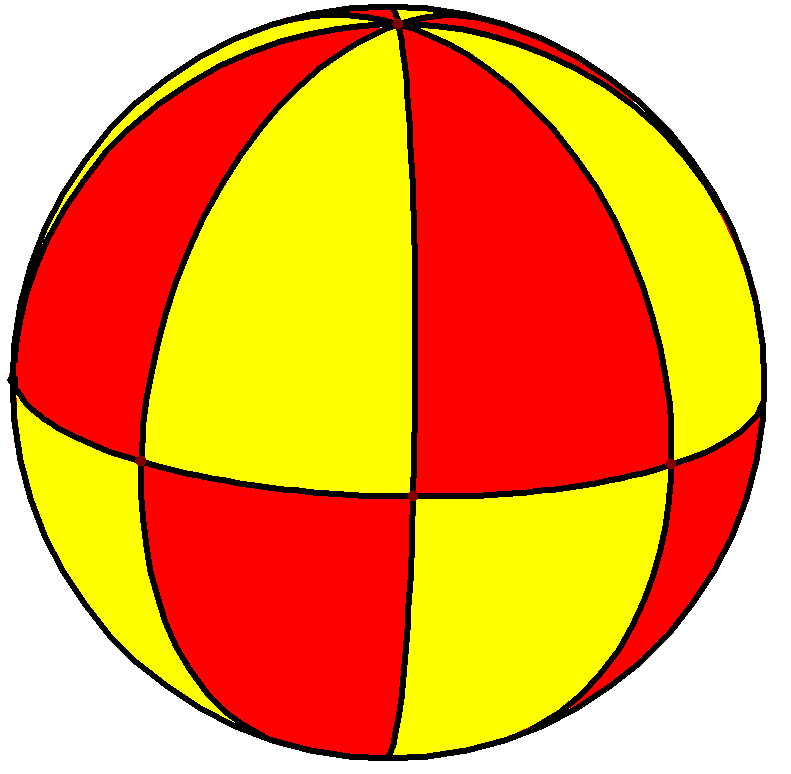
4. 3. 구면 타일링
깎은 육팔면체는 구면 타일링으로도 나타낼 수 있으며, 스테레오 투영을 통해 평면에 투영될 수 있다. 이 투영은 등각 사상으로, 각도는 보존되지만 면적이나 길이는 보존되지 않는다. 구 위의 직선은 평면에서 원호로 투영된다.
4. 4. 팔면체 대칭군
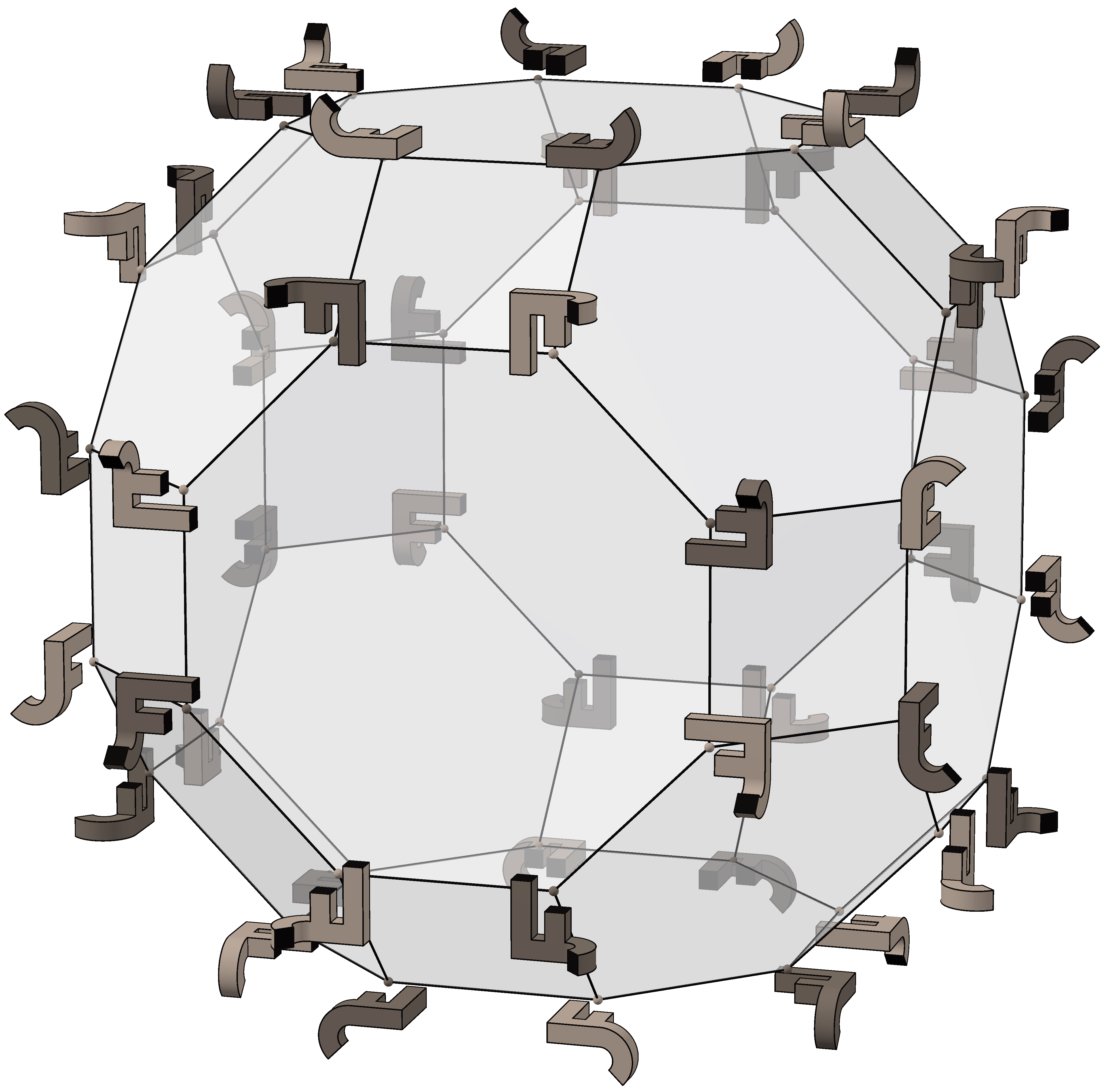
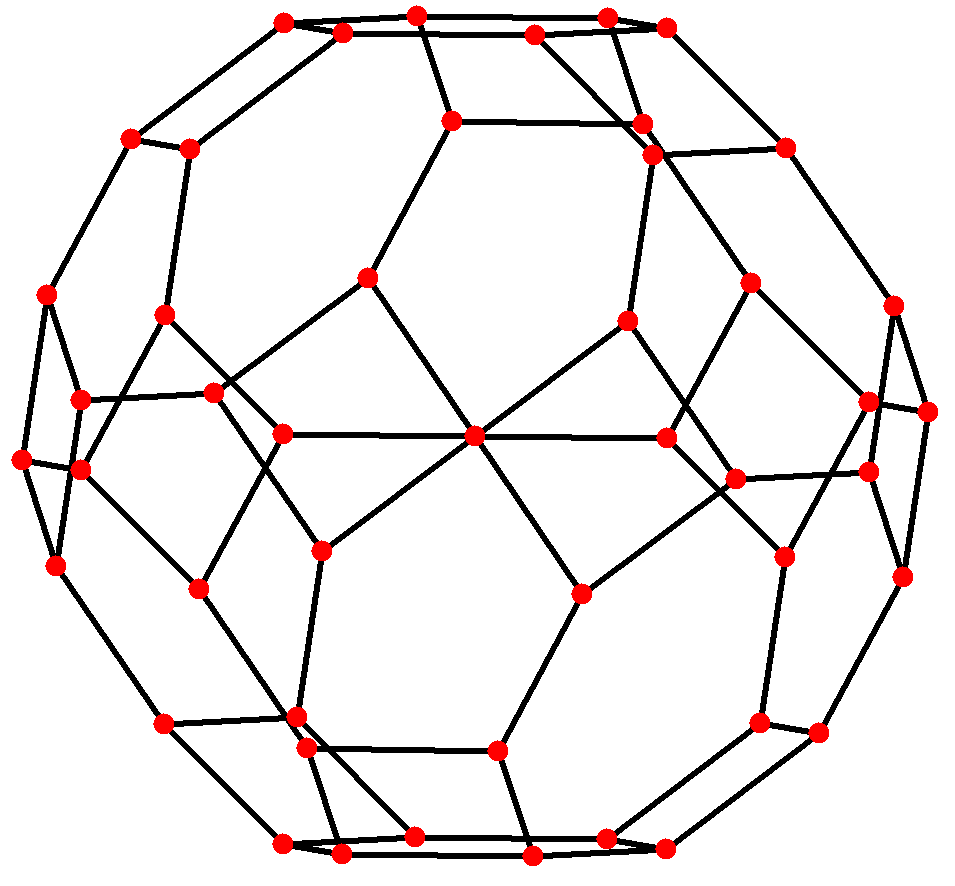
다른 많은 다면체와 마찬가지로 깎은 팔면체는 완전한 팔면체 대칭을 갖지만, 완전 팔면체 그룹과의 관계는 이보다 더 밀접하다. 48개의 꼭짓점은 그룹의 원소에 해당하며, 이중 육팔면체의 각 면은 그룹의 기본 영역이다.
오른쪽 이미지는 그룹의 48개 순열을 예시 객체(왼쪽의 밝은 JF 화합물)에 적용한 것을 보여준다. 24개의 밝은 원소는 회전이며, 어두운 원소는 그들의 반사이다.
다면체의 모서리는 그룹의 9개 반사에 해당한다.
- 팔각형과 사각형 사이의 모서리는 반대쪽 팔각형 사이의 3개 반사에 해당한다.
- 육각형 모서리는 반대쪽 사각형 사이의 6개 반사에 해당한다.
- (반대쪽 육각형 사이에는 반사가 없다.)
부분군은 깎은 팔면체의 해당 꼭짓점을 공유하는 다면체에 해당한다.
예를 들어, 24개 원소를 가진 3개의 부분군은 키랄 팔면체 대칭을 갖는 불균일한 스너브 정육면체, 피리토헤드랄 대칭을 갖는 불균일한 사각 육팔면체(칸틱 스너브 팔면체), 완전 사면체 대칭을 갖는 불균일한 깎은 팔면체에 해당한다. 12개 원소를 갖는 고유한 부분군은 교대군 A4이다. 이것은 키랄 사면체 대칭을 갖는 불균일한 정이십면체에 해당한다.
| 부분군과 해당 다면체 | ||||
|---|---|---|---|---|
| 깎은 육팔면체 tr{4,3} | 스너브 정육면체 sr{4,3} | 사각육팔면체 s2{3,4} | 깎은 팔면체 h1,2{4,3} | 정이십면체 |
| [4,3] 완전 팔면체 | [4,3]+ 키랄 팔면체 | [4,3+] 피리토헤드랄 | [1+,4,3] = [3,3] 완전 사면체 | [1+,4,3+] = [3,3]+ 키랄 사면체 |
 |  |  |  |  |
| 모든 48개 꼭짓점 | 24개 꼭짓점 | 12개 꼭짓점 | ||
4. 5. 관련 다면체
*n32[n,3]
[2,3]
[3,3]
[4,3]
[5,3]
[6,3]
[7,3]
[8,3]
[∞,3]
[12i,3]
[9i,3]
[6i,3]
[3i,3]
